本文|下图_CUDA编程之GEMM优化

篇首语：本文由编程笔记#小编为大家整理，主要介绍了CUDA编程之GEMM优化相关的知识，希望对你有一定的参考价值。

最近由于工作需要&＃xff0c;研究了一下CUDA编程中的GEMM的优化&＃xff0c;主要是学习了GEMM优化的常用方法&＃xff0c;同时自己也利用了常用优化方法动手实现了一遍GEMM优化。学习过程中主要参考了CUTLASS官方博客&＃xff0c;网上也有中文翻译版本&＃xff0c;里面有些地方翻译的可能不是很准确&＃xff0c;在阅读中文版本的时候最好能对照原文看一下&＃xff0c;在学习过程中还参考了网上的其他一些资料&＃xff1a;

1. CUDA SGEMM矩阵乘法优化笔记——从入门到cublas
2. 深入浅出GPU优化系列&＃xff1a;GEMM优化&＃xff08;一&＃xff09;

这篇文章主要想谈谈自己对GEMM优化的一些理解。

文章目录

• 前言
• Matrix类的设计
• • 为什么要设计Matrix
  • 设计思想
  • 代码实现
  
  
• GEMM优化
• • GEMM简介
  • Baseline: NaiveGEMM
  • 减少访存策略1&＃xff1a;Block分块
  • 减少访存策略2&＃xff1a;Thread分块
  • 数据预取
  
  
• 性能测试
• 结束语

由于本文的所有示例代码都是基于Matrix类来设计的&＃xff0c;所以这里有必要先讲一下Matrix类的设计。

为什么要设计Matrix

在自己手动实现GEMM优化的时候&＃xff0c;发现一个问题&＃xff1a;由于GEMM优化的时候需要对block和thread分块&＃xff0c;这样就会涉及到大量子块以及子块元素索引的计算&＃xff0c;很容易出错&＃xff0c;为了简化索引的计算和提高可读性&＃xff0c;设计了Matrix这个类型。

设计思想

在设计Matrix类的时候&＃xff0c;我参考了Pytorch的Tensor的设计思想&＃xff0c;Pytorch的作者在一篇博客中详细介绍了Tensor的设计思想&＃xff0c;我们都知道Pytorch中的Tensor类型不保存实际的数据&＃xff0c;也就意味着Tensor不负责实际数据的分配和释放&＃xff0c;真实数据的分配和释放是由Storage这个类型来操作的&＃xff0c;Tensor只是实际数据的一个逻辑视图(view)。下图来自那篇博客&＃xff0c;图中很清楚的说明了Tensor和Storage的关系。

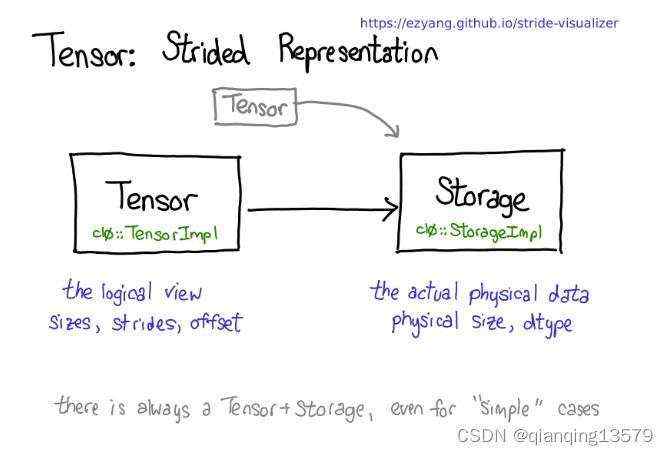
基于Pytorch的设计思想&＃xff0c;Matrix类也被设计成了Tensor一样的机制&＃xff0c;也就是Matrix不保存实际的内存数据&＃xff0c;Matrix只是实际数据的一个视图(view)。Matrix除了拥有一个数据指针外&＃xff0c;还具有两个重要的属性&＃xff1a;size和stride。通过这两个属性&＃xff0c;我们就可以很方便的访问矩阵数据了。下面我们看一下Matrix的视图机制是如何实现数据访问的。
下图表示内存中的一个4行6列的二维数组&＃xff0c;该数组按照行主序的方式在内存中连续存储(与C语言中的数组一致)&＃xff0c;所以在列这个维度上步长为1&＃xff0c;在行这个维度上的步长为6。

现在我们要从该数组中获取一个4行3列的一个子数组&＃xff0c;如下图所示&＃xff1a;

下面我们可以利用视图完成该操作。

我们让视图的数据指针指向原始数据的第3个元素&＃xff08;原始数组下标为2的元素&＃xff09;&＃xff0c;然后设置视图的size为[4,3]&＃xff0c;stride为[6,1]。如果我们要访问该子矩阵索引为(1,1)的元素&＃xff08;下图红色元素&＃xff09;&＃xff0c;则其内存索引为二维索引与stride的内积&＃xff0c;即16&＃43;11&＃61;7&＃xff0c;通过将data pointer移动7次就可以访问到该元素了。

通过上面对视图的介绍&＃xff0c;我们可以看出通过视图机制&＃xff0c;我们可以不用拷贝子数组的数据就可以很方便的访问该子数组。

代码实现

下面看一下Matrix的具体代码实现

template
class Matrix
public:
__device__ __host__ Matrix() &＃61; default;
__device__ __host__ Matrix(const Matrix &) &＃61; default;
__device__ __host__ Matrix& operator&＃61;(const Matrix &) &＃61; default;
__device__ __host__ Matrix(T *_data,int _rows,int _cols,int _strideOfRow,int _strideOfCol):
data(_data),
rows(_rows),
cols(_cols),
strideOfRow(_strideOfRow),
strideOfCol(_strideOfCol)
// 返回该矩阵所有字节数
constexpr __device__ __host__ int GetNumberOfBytes() const

return rows*cols*sizeof(T);

// 返回该矩阵元素个数
constexpr __device__ __host__ int GetNumberOfElements() const

return rows*cols;

// 访问某个元素&＃xff0c;该元素的索引为二维逻辑索引&＃xff1a;(rowIndex,colIndex)
__device__ __host__ float &operator()(int rowIndex,int colIndex)

// 计算内存索引
int memoryIndex&＃61;rowIndex*strideOfRow&＃43;colIndex*strideOfCol;
return data[memoryIndex];

// 访问某个元素&＃xff0c;该元素的索引为一维逻辑索引&＃xff1a;(Index)
__device__ __host__ float &operator()(int index)

// 转换为二维逻辑索引
int colIndex&＃61;index%cols;
int rowIndex&＃61;index/cols;
// 计算内存索引
int memoryIndex&＃61;rowIndex*strideOfRow&＃43;colIndex*strideOfCol;
return data[memoryIndex];

public:
T *data &＃61; nullptr; // 数据指针
int rows &＃61; 0;// 矩阵的行数
int cols &＃61; 0;// 矩阵的列数
int strideOfRow &＃61; 0;// 行步长
int strideOfCol &＃61; 0;// 列步长
;


1. 由于该类型需要同时在host端和device端使用&＃xff0c;所以里面的成员都需要设置为__device__ host
2. 由于该类型是一个视图类&＃xff0c;所以拷贝构造和拷贝赋值直接使用默认的就可以了&＃xff0c;不用自定义
3. 这里需要区分一下两个概念&＃xff1a;逻辑索引和内存索引&＃xff0c;通常我们访问矩阵的数据的时候都是使用的逻辑索引&＃xff0c;比如a[1][1],这里的索引(1,1)就是逻辑索引&＃xff0c;而计算机在访问实际数据的时候&＃xff0c;使用的是内存索引&＃xff0c;逻辑索引(1,1)会被转换为实际的内存索引&＃xff0c;比如上面的示例中&＃xff0c;逻辑索引(1,1)被转换为了内存索引7

有了Matrix这个类&＃xff0c;我们就可以方便的访问子矩阵的元素了。前面提到的示例可以通过下面的代码来实现&＃xff0c;其中矩阵b就表示a中黄色部分的子矩阵。


Matrix<float> a;
Matrix<float> b(a.data&＃43;2,4,3,a.strideOfRow,a.strideOfCol );// a矩阵的一个4行3列的子矩阵
a(1,1)&＃61;0;// 访问索引为(1,1)的元素&＃xff0c;实际访问的时候&＃xff0c;会转换为内存索引7&＃xff0c;然后通过data[7]访问到实际的元素


介绍了Matrix的设计之后&＃xff0c;下面我们来看一下GEMM优化。由于学习过程中主要参考了CUTLASS官方博客&＃xff0c;所以本文的GEMM优化思路与这篇博客基本相同。

GEMM简介

在高性能计算领域&＃xff0c;矩阵乘&＃xff08;GEMM&＃xff09;的优化是一个非常重要的课题。GEMM可以非常广泛地应用于航空航天、流体力
学及深度学习领域。GEMM的计算公式如下&＃xff1a;
$$C\&＃61;alphaA\ast B\&＃43;betaC$$

其中A是一个M x K的矩阵&＃xff0c;B是一个K x N的矩阵&＃xff0c;C是一个M x N的矩阵&＃xff0c;alpha和beta是标量。
为了简化计算&＃xff0c;本文中设置alpha&＃61;1.0,beta&＃61;0。上述公式变为&＃xff1a;
$$C\&＃61;A\ast B$$

Baseline: NaiveGEMM

对于GEMM计算&＃xff0c;我们很容易想到如下的实现&＃xff1a;

__global__ void NaiveGEMM(Matrix<float> A,Matrix<float> B,Matrix<float> C)


// 获取线程在网格内的索引
int row &＃61; blockIdx.y * blockDim.y &＃43; threadIdx.y;// 行
int col &＃61; blockIdx.x * blockDim.x &＃43; threadIdx.x;// 列
// 每个线程计算矩阵C的一个元素
if(row<C.rows&&col<C.cols)

float c &＃61; 0;
for (int i &＃61; 0; i < A.cols; &＃43;&＃43;i)

c &＃43;&＃61; A(row,i)*B(i,col);// 使用A的第row行乘以B的第col列

C(row,col) &＃61; c;




这种实现中&＃xff0c;每个线程使用A的一行和B的一列计算矩阵C中的一个元素。这种实现存在如下问题&＃xff1a;访存开销太大&＃xff0c;A和B矩阵的全局内存被访问了多次&＃xff0c;其中A矩阵被访问了N次&＃xff0c;B矩阵被访问了M次。下面我们以这个实现为baseline来进行GEMM的优化。

减少访存策略1&＃xff1a;Block分块

NaiveGEMM的主要问题在于访存开销太大&＃xff0c;所以下面我们主要的优化点就是要减少访存&＃xff0c;其实很容易想到的思路就是利用共享内存(Shared Memory)&＃xff0c;基本思路就是将每个block需要的A矩阵的部分和B矩阵的部分先读取到共享内存中&＃xff0c;然后再计算&＃xff0c;这样每次只需要读取一次全局内存就可以了&＃xff0c;但是这里有个问题就是由于共享内存的容量是非常有限的&＃xff0c;如果矩阵A和矩阵B规模比较大&＃xff0c;则无法一次性全部加载到共享内存&＃xff0c;所以我们需要分批加载。如下图所示&＃xff0c;在计算C矩阵的绿色子块的时候&＃xff0c;加载A和B矩阵的时候&＃xff0c;沿着K维度每次只加载下图中1和2大小的子块。

所以GEMM优化的第一步就是Block分块&＃xff1a;每个Block负责计算C矩阵的一个子块&＃xff0c;每次计算子块的时候&＃xff0c;沿着K维度分批将A和B加载到共享内存中计算乘累加。

与NaiveGEMM一样&＃xff0c;这种实现方式每个线程还是负责block中一个元素的计算。通过Block分块&＃xff0c;可以显著减少对全局内存的访问次数。假设每个Block的行大小为BM,列大小为BN,则优化后A矩阵被访问N/BN次&＃xff0c;B矩阵被访问了M/BM次。

代码实现如下&＃xff1a;

__global__ void BlockGEMM_V1(Matrix<float> A,Matrix<float> B,Matrix<float> C)

// 注意命名不要与前面的宏定义重名
const int BLOCK_M&＃61;16;// block的行数
const int BLOCK_N&＃61;16;// block的列数
const int BLOCK_K&＃61;16;
// 沿着K维度循环加载一个block中对应的A和B的数据到共享内存
float c&＃61;0.0;
for(int i&＃61;0;i<A.cols/BLOCK_K;&＃43;&＃43;i)

// 每个block对应的全局内存中的A,B子块&＃xff0c;即创建全局内存中A,B的view
Matrix<float> ASub(A.data&＃43;blockIdx.y*BLOCK_M*A.strideOfRow&＃43;i*BLOCK_K,BLOCK_M,BLOCK_K,A.strideOfRow,A.strideOfCol);
Matrix<float> BSub(B.data&＃43;i*BLOCK_K*B.strideOfRow&＃43;blockIdx.x*BLOCK_N,BLOCK_K,BLOCK_N,B.strideOfRow,B.strideOfCol);
// 将Asub,BSub加载到共享内存
// 注意&＃xff1a;这里需要将一维逻辑索引转换为多维逻辑索引&＃xff1a;stardIndex->(stardIndex/cols,stardIndex%cols)
__shared__ float A_Shared[BLOCK_M][BLOCK_K];
__shared__ float B_Shared[BLOCK_K][BLOCK_N];
int numberOfElementsPerThread&＃61;(BLOCK_K*BLOCK_M)/(blockDim.x*blockDim.y);// 每个线程需要读取多少数据
int stardIndex&＃61;numberOfElementsPerThread*(threadIdx.y*blockDim.x&＃43;threadIdx.x);// stardIndex为每个线程读取的起始索引
for(int threadIndex&＃61;0;threadIndex<numberOfElementsPerThread;&＃43;&＃43;threadIndex)

int logicalIndex&＃61;stardIndex&＃43;threadIndex;
A_Shared[logicalIndex/BLOCK_K][logicalIndex%BLOCK_K]&＃61;ASub(logicalIndex/BLOCK_K,logicalIndex%BLOCK_K);
B_Shared[logicalIndex/BLOCK_N][logicalIndex%BLOCK_N]&＃61;BSub(logicalIndex/BLOCK_N,logicalIndex%BLOCK_N);

__syncthreads();
// 每个thread计算A的一行和B的一列
for(int k&＃61;0;k<BLOCK_K;&＃43;&＃43;k)

c&＃43;&＃61;A_Shared[threadIdx.y][k]*B_Shared[k][threadIdx.x];

__syncthreads();

// 将每个线程计算好的结果写回到C矩阵
// CSub为每个线程对应的全局内存的C矩阵子块&＃xff0c;创建C矩阵的view
Matrix<float> CSub(C.data&＃43;(blockIdx.y*BLOCK_M*C.strideOfRow&＃43;blockIdx.x*BLOCK_N),BLOCK_M,BLOCK_N,C.strideOfRow,C.strideOfCol);
CSub(threadIdx.y,threadIdx.x)&＃61;c;



但是这种实现方式依旧存在访存的问题&＃xff1a;由于每个线程还是计算block中的一个元素&＃xff0c;还是存在对共享内存的反复读取&＃xff0c;虽然共享内存的速度要比全局内存快很多&＃xff0c;但是如果矩阵规模很大&＃xff0c;那这一块的访存开销还是很大。

减少访存策略2&＃xff1a;Thread分块

参考Block分块的思想&＃xff0c;我们让每个线程也计算一个子块&＃xff0c;Thread分块的基本思想与Block分块的思想相同&＃xff1a;每个线程计算一个子块&＃xff0c;计算的时候先将每个线程对应的共享内存数据读取到寄存器中&＃xff0c;然后再计算&＃xff0c;由于寄存器数量非常有限&＃xff0c;所以这里也不能一次性加载到寄存器中&＃xff0c;所以也需要分批加载&＃xff0c;为了只读取一遍共享内存&＃xff0c;我们需要采用矩阵外积的计算形式&＃xff1a;也就是每个线程计算子块的时候&＃xff0c;读取A矩阵的一列和B矩阵的一行到寄存器&＃xff0c;然后计算外积&＃xff0c;这样就只需要读取一遍共享内存就可以了。

代码实现如下&＃xff1a;

// 分块参数
#define BM 128 // block子块大小
#define BN 128
#define BK 8
#define TM 8 // thread子块大小
#define TN 8
__global__ void BlockGEMM_V2(Matrix<float> A,Matrix<float> B,Matrix<float> C)

// 每个线程的计算结果
float c[TM][TN]&＃61;0.0;
float a[TM]&＃61;0.0;
float b[TN]&＃61;0.0;
// 沿着K维度循环加载一个block中对应的A和B的数据到共享内存
for(int i&＃61;0;i<A.cols/BK;&＃43;&＃43;i)

// 每个block对应的全局内存中的A,B子块&＃xff0c;即创建全局内存中A,B的view
Matrix<float> ASub(A.data&＃43;blockIdx.y*BM*A.strideOfRow&＃43;i*BK,BM,BK,A.strideOfRow,A.strideOfCol);
Matrix<float> BSub(B.data&＃43;i*BK*B.strideOfRow&＃43;blockIdx.x*BN,BK,BN,B.strideOfRow,B.strideOfCol);
// 将Asub,BSub加载到共享内存
// 以block为128&＃xff0c;thread为8为例&＃xff1a;由于一个block有16x16&＃61;256个线程&＃xff0c;而ASub和BSub中一共有1024个元素&＃xff0c;所以每个线程加载4个元素
// 注意&＃xff1a;这里需要将一维逻辑索引转换为多维逻辑索引&＃xff1a;stardIndex->(stardIndex/cols,stardIndex%cols)
__shared__ float A_Shared[BM][BK];
__shared__ float B_Shared[BK][BN];
int numberOfElementsPerThread&＃61;(BK*BM)/(blockDim.x*blockDim.y);// 每个线程需要读取多少数据
int stardIndex&＃61;numberOfElementsPerThread*(threadIdx.y*blockDim.x&＃43;threadIdx.x);// stardIndex为每个线程读取的起始索引
for(int threadIndex&＃61;0;threadIndex<numberOfElementsPerThread;&＃43;&＃43;threadIndex)

int logicalIndex&＃61;stardIndex&＃43;threadIndex;
A_Shared[logicalIndex/BK][logicalIndex%BK]&＃61;ASub(logicalIndex/BK,logicalIndex%BK);
B_Shared[logicalIndex/BN][logicalIndex%BN]&＃61;BSub(logicalIndex/BN,logicalIndex%BN);

__syncthreads();
// 每个thread对应的共享内存中的A_Shared,B_Shared的子块&＃xff0c;即创建A_Shared,B_Shared的view
Matrix<float> ASub_Shared((float *)A_Shared&＃43;threadIdx.y*TM*BK,TM,BK,BK,1);// 每个线程对应的共享内存中A和B的子块
Matrix<float> BSub_Shared((float *)B_Shared&＃43;threadIdx.x*TN,BK,TN,BN,1);
// 每个线程执行计算
for(int k&＃61;0;k<BK;&＃43;&＃43;k)

// 先将A的一列和B的一行加载到寄存器
for(int m&＃61;0;m<TM;&＃43;&＃43;m)

a[m]&＃61;ASub_Shared(m,k);

for(int n&＃61;0;n<TN;&＃43;&＃43;n)

b[n]&＃61;BSub_Shared(k,n);

// 使用寄存器计算
for(int m&＃61;0;m<TM;&＃43;&＃43;m)

for(int n&＃61;0;n<TN;&＃43;&＃43;n)

c[m][n]&＃43;&＃61;a[m]*b[n];



__syncthreads();

// 将每个线程计算好的结果写回到C矩阵
// CSub为每个线程对应的全局内存的C矩阵子块&＃xff0c;创建C矩阵的view
Matrix<float> CSub(C.data&＃43;((blockIdx.y*BM&＃43;threadIdx.y*TM)*C.strideOfRow&＃43;blockIdx.x*BN&＃43;threadIdx.x*TN),TM,TN,C.strideOfRow,C.strideOfCol);
for(int m&＃61;0;m<TM;&＃43;&＃43;m)

for(int n&＃61;0;n<TN;&＃43;&＃43;n)

CSub(m,n)&＃61;c[m][n];





数据预取

通过前面的优化相对于NaiveGEMM已经有了很大提高了。下面我们分析一下BlockGEMM_V2的实现&＃xff0c;在CUTLASS官方博客中的Software Pipelining一节中提到了BlockGEMM_V2这种实现方式存在这样的问题&＃xff1a;每个线程按照“访存1—计算1—访存2—计算2—…—访存n—计算n”的顺序执行&＃xff0c;这种执行方式每次计算单元都需要等待访存&＃xff0c;而访存的延迟通常都是比较大的&＃xff0c;所以这种实现会存在较大的访存延迟&＃xff0c;为了减少访存延迟&＃xff0c;Software Pipelining一节中提到了将下一次访存和上一次计算并行&＃xff0c;这样可以掩盖访存的延迟。

这种优化方式也叫数据预取。代码实现如下&＃xff1a;

// 分块参数
#define BM 128 // block子块大小
#define BN 128
#define BK 8
#define TM 8 // thread子块大小
#define TN 8
__global__ void BlockGEMM_V3(Matrix<float> A,Matrix<float> B,Matrix<float> C)

// 每个线程的计算结果
float c[TM][TN]&＃61;0.0;
float a[TM]&＃61;0.0;
float b[TN]&＃61;0.0;
// 此时需要的共享内存是原来的2倍
// 注意&＃xff1a;读取和写入的时候第一个维度的索引是交错进行的
__shared__ float A_Shared[2][BM][BK];
__shared__ float B_Shared[2][BK][BN];
// 预取(先读取第一个BK)
Matrix<float> ASub(A.data&＃43;blockIdx.y*BM*A.strideOfRow&＃43;0*BK,BM,BK,A.strideOfRow,A.strideOfCol);
Matrix<float> BSub(B.data&＃43;0*BK*B.strideOfRow&＃43;blockIdx.x*BN,BK,BN,B.strideOfRow,B.strideOfCol);
int numberOfElementsPerThread&＃61;(BK*BM)/(blockDim.x*blockDim.y);
int stardIndex&＃61;numberOfElementsPerThread*(threadIdx.y*blockDim.x&＃43;threadIdx.x);// stardIndex为每个线程读取的起始索引
for(int threadIndex&＃61;0;threadIndex<numberOfElementsPerThread;&＃43;&＃43;threadIndex)

int logicalIndex&＃61;stardIndex&＃43;threadIndex;
A_Shared[0][logicalIndex/BK][logicalIndex%BK]&＃61;ASub(logicalIndex/BK,logicalIndex%BK);
B_Shared[0][logicalIndex/BN][logicalIndex%BN]&＃61;BSub(logicalIndex/BN,logicalIndex%BN);

__syncthreads();
// 沿着K维度循环加载剩下的数据
int indexOfRead,indexOfWrite;
bool indexFlag&＃61;false;// 辅助变量&＃xff0c;用来计算索引
for(int i&＃61;1;i<A.cols/BK;&＃43;&＃43;i)

// 计算索引&＃xff0c;indexOfRead和indexOfWrite每次循环会交替变换&＃xff0c;i&＃61;1时为indexOfRead&＃61;0,indexOfWrite&＃61;1&＃xff0c;i&＃61;2时为indexOfRead&＃61;1,indexOfWrite&＃61;0
indexOfRead &＃61; (int)indexFlag; // 读索引&＃xff0c;即本次循环读取A_Shared[indexOfRead,:,:]和B_Shared[indexOfRead,:,:]中的数据执行计算
indexOfWrite &＃61; 1-indexOfRead; // 写索引&＃xff0c;即预取下一次计算需要的数据到A_Shared[indexOfWrite,:,:]和B_Shared[indexOfWrite,:,:]中
// 每个线程执行计算
Matrix<float> ASub_Shared(((float *)A_Shared&＃43;indexOfRead*BM*BK)